Nassim Taleb calls Nate Silver totally clueless about probability: who is right about election forecasting?

11 Oct 2020

Background

Perhaps lost in the whirlwind of presidential name-calling, a lesser-known multi-year old feud has resurfaced on Twitter this election season. Nate Silver is the founder of FiveThirtyEight and is a popular statistician frequently called upon by media members to give commentary and expertise on election forecasting. Nassim Taleb is a statistician/quant turned philosopher, perhaps most well known for authoring the book “The Black Swan”. He is second most well known for calling people names on Twitter. In this 2018 instance he seemed to take issue with FiveThirtyEight’s election forecasts, saying that “klueless Nate Silver” “doesn’t know how math works”, among a host of other insults. Silver responded that Taleb was an “intellectual-yet-idiot”, an phrase coined by Taleb himself. Ouch. A litany of statisticans, mathematicians, and data scientists came out of the woodwork to take sides. Taleb himself doubled down on Oct. 10, 2020, again calling Silver “totally clueless”.

In this article I take a look behind the mathematical premises of Taleb’s arguments, and give intuitive explanations of why or why not they hold up. In short, while Taleb’s math is sound, he still manages to miss the mark by ignoring the nuance of Silver’s forecasts.

Taleb’s main gripe is that forecasters change their opinion too much over time. Take a look at FiveThirtyEight’s forecast from the 2016 presidential election, where the probability of Clinton winning peaked at 90%, and hit a low of 50%.

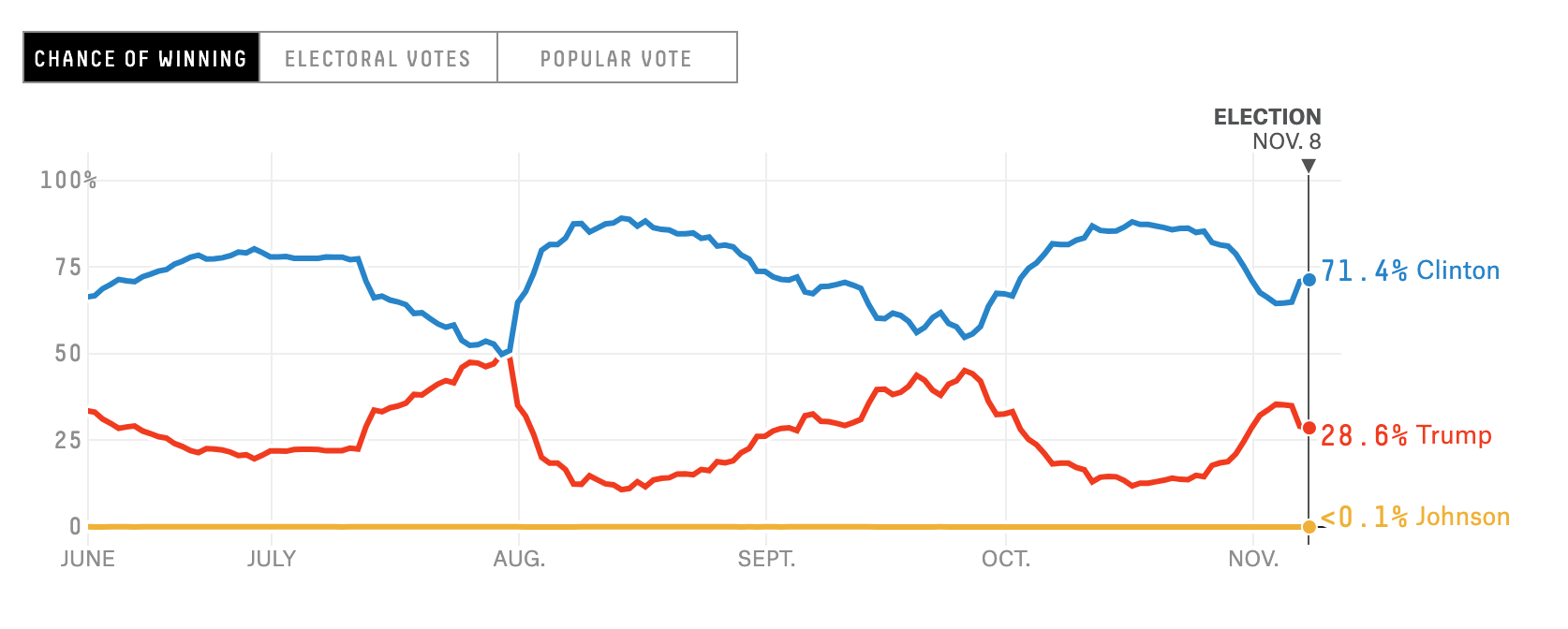
Taleb insists that Clinton never should’ve received a probability of winning of 90%. Even if polls were heavily in favor of Clinton at the time, he says Silver should’ve taken into account the uncertainty that polls would change over the next few months leading up to the election, or the possibility of major news breaking. If Silver had factored in the “unknown unknowns” his forecast should’ve been closer to 50%. In essence, this single number should reflect all current and future uncertainty. Taleb constructs this argument by way of quantitative finance, which perhaps led to him and traditional statisticians talking past each other. In the following sections I step through his argument in intuitive terms.

Premise 1: If you give a probability, you must be willing to wager on it

A well known truth to economists, quants, and traders: if I tell you a number, I must be willing to transact at that number. If I tell you the fair value of this house is 500,000, I must be willing to buy AND sell at that price. Otherwise, the number I gave you is meaningless. Likewise, if I tell you the probability of Biden winning this election is 73%, I must be willing to pay 0.73 to make the following wager: if Biden wins I receive 1, if he loses I receive 0.

This is important because it turns the predicted probabilities into a tradeable financial instrument known as a binary option. If the prediction is 50%, I can buy the option at $0.50. If the prediction moves to 65%, I can now sell the option at 0.65, turning a 0.15 profit.

This brings us to another important principle known as the no-arbitrage condition. If the election predictions are accurate, there should be no way for a trader to make guaranteed money by trading this option. To give an illustrative example, let’s say that we live in an unchanging world where the probability of Candidate A winning is static at 50%. If a pollster does not report a static forecast day after day, he will create an arbitrage opportunity. We will sell when the prediction is above 50%, and buy below.

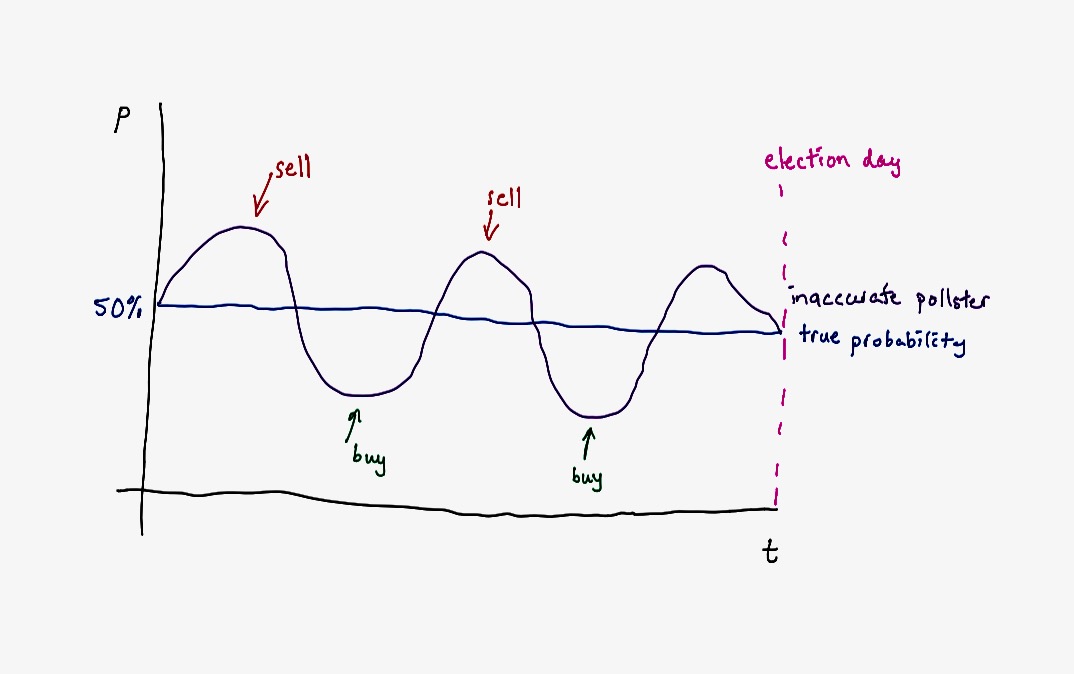
OK, so now we’ve established that if an arbitrage condition exists, then the pollster is wrong and should not have made that prediction in the first place. Still, it’s not obvious that there’s an arbitrage condition within Silver’s predictions yet (remember, the trader doesn’t have access to an oracle, and only has the same information available to him as the pollster). There’s two more building blocks that we need in order to establish an arbitrage condition.

Premise 2: High probability implies high confidence

To paraphrase Taleb, if I tell you an event has a 0% chance of occurring, I cannot change my mind and tell you tomorrow it now has a 50% chance of occurring. Otherwise I shouldn’t have told you it has a 0% chance in the first place. Probability and confidence are inextricably linked, and the number a pollster predicts should encapsulate both. To go to the other extreme, if the uncertainty is extremely high (and therefore confidence low), it does not matter what the polls today are saying. I should give both candidates a 50% chance of winning, because I am admitting the extremely likely possibility that an external event will happen that will invalidate today’s polls. To put it in technical terms, maximum uncertainty implies maximum entropy, and the maximum entropy distribution on the [0, 1] interval is the uniform distribution, which has a mean at .5. The following figure (from this paper) shows the relationship between probability (x-axis) and volatility (y-axis) under a specific option pricing formulation.

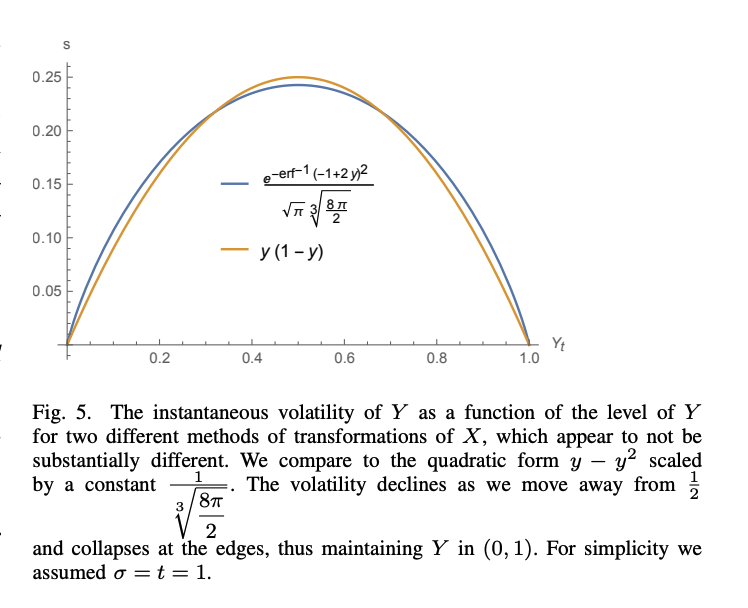
At this point we are suspecting something doesn’t look right with FiveThirtyEight’s predictions, as they seem to have both high volatility and high probability, which contradict each other. Where is the threshold though? How can we prove that the volatility is too high?

Premise 3: All traded probabilities must be martingales

Now we’re going to go a little bit technical and show that a no-arbitrage condition was likely violated. The basic construction is as follows:

1. In order to satisfy the no-arbitrage condition, all information must be “priced in” into the pollster’s current prediction.
2. Therefore, the time series of predictions must be a martingale.
3. Martingales cannot show trending or mean-reverting behavior, therefore Silver’s predictions violated the martingale property, and therefore the no-arbitrage condition.

The definition of a martingale is a stochastic process

\[X_1, X_2, ... X_t\]

that satisfies

\[E[X_{t+1} | X_1, ... ,X_t] = X_t\]

To quote Andrew Gelman,

In non-technical terms, the martingale property says that knowledge of the past will be of no use in predicting the future…One implication of this is that it should be unlikely for forecast probabilities to change too much during the campaign (Taleb, 2017). Big events can still lead to big changes in the forecast: for example, a series of polls with Biden or Trump doing much better than before will translate into an inference that public opinion has shifted in that candidate’s favor. The point of the martingale property is not that this cannot happen, but that the possibility of such shifts should be anticipated in the model, to an amount corresponding to their prior probability. If large opinion shifts are allowed with high probability, then there should be a correspondingly wide uncertainty in the vote share forecast a few months before the election, which in turn will lead to win probabilities closer to 50%.

In other words, all information is already priced into the current market. If it were not so, a trader could make money by taking advantage of the information that is not priced in already. So last thing we need to check: is it likely that Silver’s predictions have the martingale property? It is not in dispute that the answer is no…it shows clear mean-reversion behavior and can be validated by a statistical test of the martingale hypothesis (for example, a Kolmogorov-Smirnov test). It seems that Taleb’s math is sound here. So where did he go wrong?

Where Taleb missed the mark

I believe Nate Silver is answering a subtly different question with his election forecasts. Each data point that Silver produces is answering the question: if the election were to happen today, what is the probability of each candidate winning? I argue that this is a valid and useful formulation. To put it slightly differently: if the question is “Who will win the election on Nov. 3?”, which of the following answers is more satisfying?

• “If nothing else changes between now and the election, Joe Biden has a 85% chance of winning.” (Silver’s argument)
• “I dunno, anything could happen between now and the election, I give neither candidate chances much more than 50%.” (Taleb’s argument)

It is a valid criticism that perhaps Silver is not very clear on explaining what his numbers represent, and therefore the media misreports his predictions. Still, I wager that most people would find the first answer more useful. In this interpretation, the “financial instrument” is a binary option that expires every day. Thefore the time series of Silver’s predictions is not interpretable as a martingale, as it strings together the price of a completely different instrument every day.

It is also a valid criticism that Silver’s predictions prior to Nov. 3 mean absolutely nothing, whereas in the Taleb formulation it has a natural interpretation as the betting odds for each candidate. Silver has explicitly stated that he only judges his models based on his finalized prediction. To that end, his models are extremely well calibrated, i.e., when he says something has a 50% chance of happening it actually does happen 50% of the time.

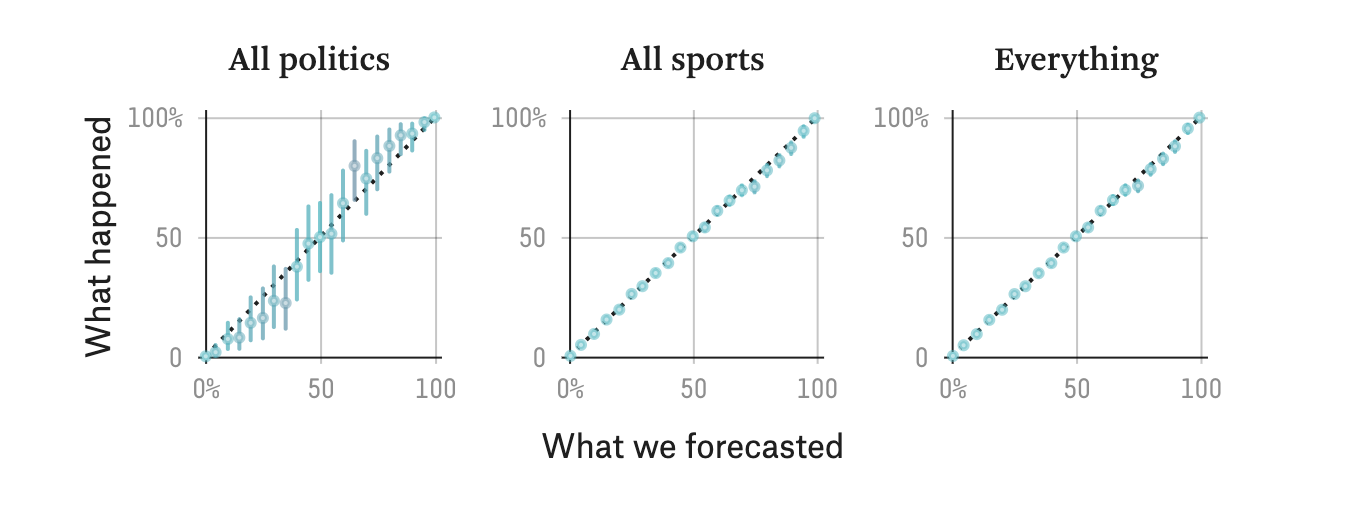
In conclusion, Taleb and Silver should be having a philosophical debate on what pollsters’ numbers actually mean, and stay away from the useless distraction of calling each other names on Twitter.

Update (10/12/2020)

Andrew Gelman, Aubrey Clayton, Dhruv Madeka and many other statisticians respond and give their thoughts: https://statmodeling.stat.columbia.edu/2020/10/12/more-on-martingale-property-of-probabilistic-forecasts-and-some-other-issues-with-our-election-model/

Update 2 (11/3/2020)

• Nassim Taleb responds to this post on Twitter
• Hacker News discussion